Basic Graphs

Graphite provides two types for graphs: UGraph for undirected graphs and DGraph for directed graphs.

Lets represent some graphs.

Undirected graphs

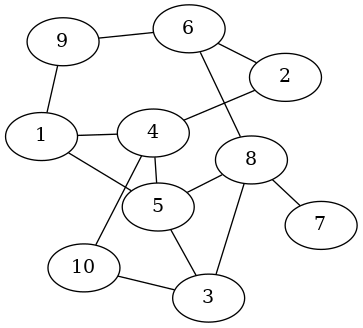
myGraph :: UGraph Int ()
myGraph = fromEdgesList
    [ 1 <-> 4
    , 1 <-> 5
    , 1 <-> 9
    , 2 <-> 4
    , 2 <-> 6
    , 3 <-> 5
    , 3 <-> 8
    , 3 <-> 10
    , 4 <-> 5
    , 4 <-> 10
    , 5 <-> 8
    , 6 <-> 8
    , 6 <-> 9
    , 7 <-> 8
    ]

The type UGraph Int () here means that this is an undirected graph UGraph, with vertices of type Int and edges with attributes of type (), that is, edges with no attributes on them.

The <-> operator constructs an Undirected Edge between two vertices.

The fromEdgesList function constructs an UGraph from a list of Edges.

Directed Graphs

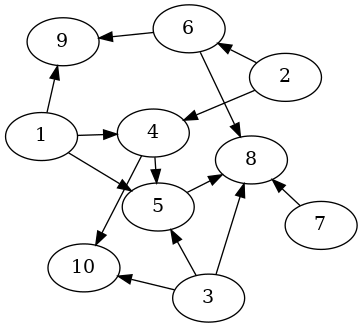
myGraph :: DGraph Int ()
myGraph = fromArcsList
    [ 1 --> 4
    , 1 --> 5
    , 1 --> 9
    , 2 --> 4
    , 2 --> 6
    , 3 --> 5
    , 3 --> 8
    , 3 --> 10
    , 4 --> 5
    , 4 --> 10
    , 5 --> 8
    , 6 --> 8
    , 6 --> 9
    , 7 --> 8
    ]

The type DGraph Int () here means that this is a directed graph DGraph, with vertices of type Int and edges with attributes of type (), that is, edges with no attributes on them.

The --> operator constructs a Directed edge (a.k.a. an Arc) between to vertices.

The fromArcsList function constructs a DGraph from a list of Arcs.

Other vertex types

Graphite can use any Hashable type as the vertices of a graph, this way we could have a graph of Ints, Floats, Bools, Chars, Strings, ByteStrings, Text and more.

Take for instance this undirected graph with Float vertices (parenthesis for clarity):

myGraph :: UGraph Float ()
myGraph = fromEdgesList [(1.3 <-> 2.5), (3.4 <-> 6.8), (2.5 <-> 4.4)]

Or this directed graph with String vertices:

myGraph :: DGraph String ()
myGraph = fromArcsList ["Paper" --> "Rock", "Rock" --> "Scissors", "Scissors" -> "Paper"]

Edges with attributes

By using the <-> and --> constructors, the resulting Edges and Arcs have attributes of type (). If we need edges with some attributes like weights or labels for example, we could use the Edge and Arc data constructors directly.

Lets build a graph of cities and the distances in kilometers between them:

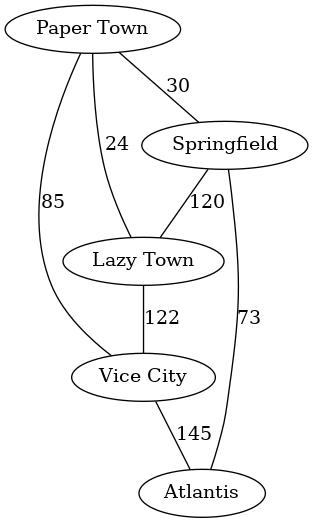
cities :: UGraph String Int
cities = fromEdgesList
    [ Edge "Paper Town" "Springfield" 30
    , Edge "Springfield" "Lazy Town" 120
    , Edge "Paper Town" "Vice City" 85
    , Edge "Vice City" "Atlantis" 145
    , Edge "Atlantis" "Springfield" 73
    , Edge "Lazy Town" "Vice City" 122
    , Edge "Lazy Town" "Paper Town" 24
    ]

If the roads between those cities are one way only, we should use Arcs instead of Edges and form a directed graph like so:

cities :: DGraph String Int
cities = fromArcsList
    [ Arc "Paper Town" "Springfield" 30
    , Arc "Springfield" "Lazy Town" 120
    , Arc "Paper Town" "Vice City" 85
    , Arc "Vice City" "Atlantis" 145
    , Arc "Atlantis" "Springfield" 73
    , Arc "Lazy Town" "Vice City" 122
    , Arc "Lazy Town" "Paper Town" 24
    ]

The edge's attributes can be of any type, so we could for instance label them by using String:

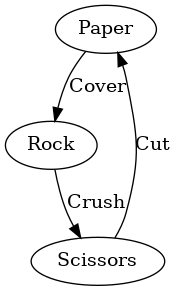
myGraph :: DGraph String String
myGraph = fromArcsList
    [ Arc "Paper" "Rock" "Cover"
    , Arc "Rock" "Scissors" "Crush"
    , Arc "Scissors" "Paper" "Cut"
    ]

Complex graphs - complex vertices, complex edges

Remember that graphite can use any Hashable data type as vertices, so we could define our own data types, make them instances of Hashable and use them as vertices.

Edge attributes on the other hand have no restriction and can be of any type; Though some functions will require the attributes to be instances of the Weighted or Labeled type classes if the nature of the algorithm requires it (like when computing shortest paths).

Lets try this out. First define some data types:

{-# LANGUAGE DeriveGeneric #-}

import GHC.Generics (Generic)
import Data.Hashable

-- Data type for vertices
data Element
    = Paper
    | Rock
    | Scissors
    deriving (Show, Ord, Eq, Generic)

instance Hashable Element


-- Data type for edge attributes
data Action
    = Cover
    | Crush
    | Cut
    deriving (Show, Ord, Eq)

Although we could define Hashable instances manually, here we go for the automatic generation of instances by leveraging Generic.

Now define a graph with vertices of type Element and edge attributes of type Action:

myGraph :: DGraph Element Action
myGraph = fromArcsList
    [ Arc Paper     Rock        Cover
    , Arc Rock      Scissors    Crush
    , Arc Scissors  Paper       Cut
    ]

Record vertices

By using the same approach it's possible to define data types with record syntax like so:

{-# LANGUAGE DeriveGeneric #-}

import GHC.Generics (Generic)
import Data.Hashable

data City = City
    { name :: String
    , major :: String
    , population :: Int
    } deriving (Show, Ord, Eq, Generic)

instance Hashable City

Write a couple instances:

lazyTown, springfield, southPark :: City

lazyTown = City "Lazy Town" "Milford Meanswell" 12
springfield = City "Springfield" "Joe Quimby" 30720
southPark = City "South Park, Colorado" "McDaniels" 2540

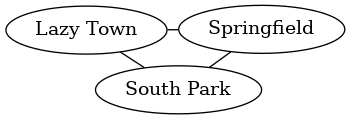
And finally use them in a graph:

cities :: UGraph City ()
cities = fromEdgesList
    [ lazyTown <-> springfield
    , springfield <-> southPark
    , southPark <-> lazyTown
    ]

Working with graph-type independence

When the type of the graph (directed/undirected) is irrelevant, the Graph type class provides a graph-type polymorphic API to work with.

In the graph-type generic interface you work with tuples and triples to represent edges, as opposed to the Edge and Arc types of the graph-type specific interfaces.

Tuples represent edges (directed or undirected, depending on the concrete graph type) with attributes of type unit ().

The following are graphs with edges defined as tuples and with attributes of type () (note how we insert edges described as the vertices they connect to the empty graph) :

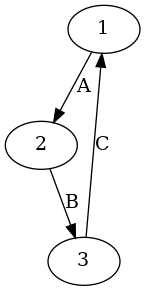
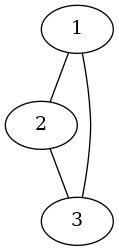
someUndirectedGraph :: UGraph Int ()
someUndirectedGraph = insertEdgePairs [(1, 2), (2, 3), (3, 1)] empty

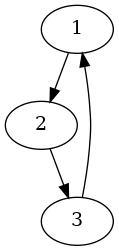
someDirectedGraph :: DGraph Int ()
someDirectedGraph = insertEdgePairs [(1, 2), (2, 3), (3, 1)] empty

Triples represent edges (directed or undirected, depending on the concrete graph type) where the third element is the edge attribute.

The following are graphs with edges defined as triples and with attributes of type String:

someUndirectedGraph :: UGraph Int String
someUndirectedGraph = insertEdgeTriples [(1, 2, "A"), (2, 3, "B"), (3, 1, "C")] empty

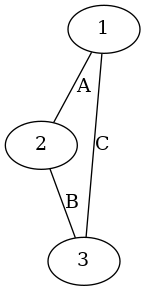
someDirectedGraph :: DGraph Int String
someDirectedGraph = insertEdgeTriples [(1, 2, "A"), (2, 3, "B"), (3, 1, "C")] empty